수리학/동수역학

유동의 정의와 분류

• 유속은 단면의 위치에 따라 다르나 일반적으로 단면 전체에 대한 평균값 사용. =평균 유속(mean velocity)
• 유선(stream line) : 임의 순간에 각 점의 속도벡터에 접하는 곡선
• 유적선(pathline, path of particle) : 유체 입자 실제의 이동 경로

연속 방정식

수직한 단면에 변화하는 흐름이 통과하는 경우

사각형 단면에 변화하는 흐름이 통과하는 경우

$dQ=Vbdy=aybdy$

$\therefore Q=\underset{0}{\overset{h}{\int }}abydy={[ab\cdot \frac{y^2}{2}]}_0^h$

평균 유속 $V=\frac{Q}{A}=\frac{\frac{ab{h}^2}{2}}{bh}=\frac{ah}{2}$
틀:-

원형 단면에 변화하는 흐름이 통과하는 경우

$dQ=udA=u\cdot 2\pi rdr$

$\begin{array}{cc}Q& =\underset{A}{\int }dQ=\underset{0}{\overset{R}{\int }}u\cdot 2\pi rdr\\ & =2\pi \underset{0}{\overset{R}{\int }}{u}_c(1-\frac{r^2}{R^2})rdr\\ & =\frac{u_c\pi R^2}{2}\end{array}$

유속 $V=\frac{Q}{A}=\frac{1}{2}{u}_c$

베르누이 방정식

펌프

펌프에 의한 동력

$P_p=\gamma Q{E}_p$

펌프의 효율

${\eta }_p=\frac{P_p}{P_{pact}}(\text{펌 프 의 효 율 }=\frac{\text{이 론 동 력 }}{\text{실 제 동 력 }}),P_{pact}=\frac{P_p}{{\eta }_p}$

펌프에 대해 요구되는 실제 동력은 손실로 인해 이론 동력보다 커야함.

터빈

터빈에 의한 동력

$P_T=\gamma Q{E}_T$

터빈의 효율

${\eta }_T=\frac{P_{Tact}}{P_T}(\text{터 빈 의 효 율 }=\frac{\text{실 제 동 력 }}{\text{이 론 동 력 }}),P_{Tact}={\eta }_T{P}_T$

터빈은 유체로부터 동력을 얻어내는 경우이므로, 터빈에서 출력되는 동력은 실제 동력보다 작다.

동수경사선과 에너지 경사선

• 에너지 경사선(Energy Grade Lines; E.G.L) : 총 에너지 수두. H의 높이와 같다.
  • 완전유체에서는 마찰에 의한 에너지 손실이 없으므로 H값 일정(에너지선은 기준면과 평행)
  • $EGL=\frac{V^2}{2g}+\frac{p}{\gamma }+z=H$
• 동수경사선(Hydraulic Grade Lines; H.G.L) : 위치수두와 압력수두 합을 연결한 선
  • 유속 감소에 따라 서서히 증가
  • $HGL=\frac{p}{\gamma }+z=EGL-\frac{V^2}{2g}$

베르누이 정리의 응용

토리첼리의 정리

소오리피스로부터의 유출

♣♣♣

$\frac{p_1}{\gamma }+\frac{{V_1}^2}{2g}+z_1=\frac{p_2}{\gamma }+\frac{{V_2}^2}{2g}+z_2$

$0+0+z_1=0+\frac{{V_2}^2}{2g}+z_2$

$V_2=\sqrt{2g(z_1-z_2)}=\sqrt{2gh}=V_{id}$(이론 유속)

$V_{act}=C_v{V}_{id}$

• C_v : 유속계수

$C_c=\frac{A_{vc}}{A_2}\approx (0.6\le C_c\le 0.7)$

$Q_{id}=A_2{V}_{id}=A_2\sqrt{2gh}$

$\begin{array}{cc}{Q}_{act}& =A_{vc}{V}_{act}\\ & =C_c\cdot C_v\cdot A_2\cdot V_{id}\\ & =C_d\cdot Q_{id}\end{array}$

유량계수 $C_d=C_c\cdot C_v$

실제 유량 $Q_{act}=C_d\cdot A_{vc}\sqrt{2gh}$

작은 오리피스는 수량을 측정하거나 조절할 목적으로 쓰임.

피토관

$\frac{p_1}{\gamma }+\frac{{V_1}^2}{2g}+z_1=\frac{p_2}{\gamma }+\frac{{V_2}^2}{2g}+z_2$

양변에 γ를 곱하면 압력을 나타내는 항으로 표현할 수 있다.

$\frac{\rho {V_1}^2}{2}+p_1+\gamma z_1=\frac{\rho {V_2}^2}{2}+p_2+\gamma z_2$

$\frac{\rho V^2}{2}+p+\gamma z=constant$

동압력(유속에 의한 압력) + 정압력 + 위치압력

오른쪽 그림에서 물체 선단에는 속도가 0이 되는 정체점 S가 생긴다. O와 S에 베르누이 정리를 쓰면
$\frac{\rho {V_0}^2}{2}+p_0=\frac{\rho {V_s}^2}{2}+p_s$

$p_s=p_0+\frac{\rho {V_0}^2}{2}$

정체점에서의 압력 = 정압력 + 동압력 = 총압력

총압력과 정압력을 구하고 이것으로부터 점유속을 측정하는 장치를 피토관이라 함.

왼쪽 관이 피토관이며, 관 내 유속은 $V=\sqrt{2g\mathrm{\Delta }h}$

벤추리미터

목 부분에서 관이 축소되어 속도는 증가하고 압력이 감소됨. 이때의 압력강하를 측정하여 유량을 구하는 장치.

어려울 것 없이 베르누이 방정식, 유량, 압력의 관계를 이용하면 됨. 식 외울 필요 없음.

$\frac{{v_1}^2}{2g}+\frac{p_1}{\gamma }+z_1=\frac{{v_2}^2}{2g}+\frac{p_2}{\gamma }+z_2$

$\frac{{v_2}^2-{v_1}^2}{2g}=\frac{p_1-p_2}{\gamma }$

$v_1=\frac{A_2}{A_1}{v}_2$, $\frac{p_1-p_2}{\gamma }=(\frac{{\gamma }_m}{\gamma }-1)h$

$\begin{array}{cc}{v}_2& =\frac{1}{\sqrt{1-{A_2}^2/{A_1}^2}}\sqrt{2gh(\frac{{\gamma }_m}{\gamma }-1)}\\ & =\frac{A_1}{\sqrt{{A_1}^2-{A_2}^2}}\sqrt{2gh(S-1)}\\ \end{array}$

$Q=A_2{v}_2=\frac{A_1{A}_2}{\sqrt{{A_1}^2-{A_2}^2}}\sqrt{2gh(S-1)}$

실제 유량은 유량계수 C_d를 곱해서 구함.

$Q^{\prime }=C_{d}Q$

운동량 방정식

검사체적 내 물질에 작용하는 모든 힘 $\sum \overrightarrow{F}$

= 검사체적 내의 질량에 작용하는 체력(body force) + 검사표면에 작용하는 모든 표면력(surface force)

정상류에 대하여, (가정 : 정상류, 유속은 단면 내에서 일정)

$\sum \overrightarrow{F}=\sum _{out}(\rho Q)\overrightarrow{V}-\sum _{in}(\rho Q)\overrightarrow{V}$

정지판에 미치는 충격력

♣♣♣

분류가 고정된 수직평판에 작용하는 경우

질량 보존 법칙 ${\rho }_1{V}_1{A}_1+{\rho }_2{V}_2{A}_2={\rho }_0{V}_0{A}_0$

비압축성 유체이면 $Q_1+Q_2=Q_0$

운동량 방정식 $\sum F_x=\sum _{out}(\rho V_{n}A)V_x-\sum _{in}(\rho V_{n}A)V_x$

x방향 수평력은 - R_x 뿐이고, (V_x)_out = 0이므로

$-R_x=-\rho Q{V}_0$

경사진 분류가 고정된 수직평판에 작용하는 경우

$V_1=V\sin \theta ,V_2=0$이므로

$F=\frac{{\gamma }_w}{g}QV\sin \theta =\frac{{\gamma }_w}{g}A{V}^2\sin \theta$

$\therefore F=\frac{{\gamma }_w}{g}A{V}^2\sin \theta$

분류가 곡면판에 충돌(θ < 90도)

x방향에 대해서 V₁ = V, V₂ = V cos θ이므로

$F_x=\frac{{\gamma }_w}{g}Q(V-V\cos \theta )=\frac{{\gamma }_w}{g}QV(1-\cos \theta )=\frac{{\gamma }_w}{g}A{V}^2(1-\cos \theta )$

$\therefore F_x=\frac{{\gamma }_w}{g}A{V}^2(1-\cos \theta )$

y방향에 대해서 V₁ = 0, V₂ = V sin θ이므로

$F_y=\frac{{\gamma }_w}{g}Q(0-V\sin \theta )=-\frac{{\gamma }_w}{g}QV\sin \theta =-\frac{{\gamma }_w}{g}A{V}^2\sin \theta$

$\therefore F_y=-\frac{{\gamma }_w}{g}A{V}^2\sin \theta$

충격력 $F=\sqrt{{F_x}^2+{F_y}^2}$

$\alpha ={\tan }^{-1}\left(\frac{F_y}{F_x}\right)$

분류가 곡면판에 충돌(θ = 180도)

$\cos \theta =\cos (180-{\theta }_0)=-\cos {\theta }_0$

$F=\frac{{\gamma }_w}{g}Q(V+V\cos {\theta }_0)=\frac{{\gamma }_w}{g}QV(1+\cos {\theta }_0)$

여기서 $\cos \theta =\cos 180^{\circ }=-1$이므로

$F=\frac{2{\gamma }_w}{g}QV=\frac{2{\gamma }_w}{g}A{V}^2$

오일러의 운동 방정식과 연속 방정식

1차원 흐름의 연속 방정식

• 정상류이면 ρVA = 일정
• 정상류이면서 비압축성이면 VA = Q = 일정

연속방정식의 일반형

• 정상류이면 $u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y}+w\frac{\partial \rho }{\partial z}+\rho (\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z})=0$
• 정상류이면서 비압축성이면 $\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$

오일러 운동방정식의 적분과 베르누이 방정식

1차원 베르누이 방정식

• 1차원 오일러 운동방정식을 적분하면 베르누이 방정식(에너지 방정식)
• $\frac{V^2}{2g}+\frac{p}{\gamma }+z=H$
• 속도 수두 + 압력 수두 + 위치 수두 = 전수두
• velocity head + pressure head + elevation head = total head
• 주의점(가정)
  • 정상류
  • 비압축성
  • 비점성(마찰 없음)
  • 한 유선을 따른 흐름

속도포텐셜과 항력

♣♣

항력(Drag force; D) : 흐르는 유체 속에 있는 물체가 받는 힘을 유체의 저항력 또는 항력이라 함.

$D=C_{d}A\frac{\rho V^2}{2},C_d=\frac{24}{Re}$

• A : 흐름 방향의 물체 투영 면적

오리피스와 위어

오리피스 유량 계산

작은 오리피스

수량을 측정하거나 조절할 목적으로 사용.

오리피스 수두 오차와 유량 오차의 관계

$Q=CA\sqrt{2gH}$를 H에 대해 미분하면,

$\frac{dQ}{dH}=CA\sqrt{2g}\cdot \frac{1}{2}{H}^{-\frac{1}{2}}$을 유량 Q로 나누어주면

$\frac{dQ}{Q}=\frac{CA\sqrt{2g}\cdot \frac{1}{2}{H}^{-\frac{1}{2}}dH}{CA\sqrt{2gH}}=\frac{1}{2}\frac{dH}{H}$

$\therefore \frac{dQ}{Q}=\frac{1}{2}\frac{dH}{H}$

사각형 위어

Francis 유량 산정 공식(실험식)

♣♣

수축에 의한 유량 감소를 고려한 식(C = 0.623)으로 가정.

$Q=1.84(b-\frac{nh}{10})h^{\frac{3}{2}}$

• n : 단수축 수(양단이면 2, 일단이면 1, 수축이 없으면 0)

광정 위어

broad crest weir. 월류수심 h에 비해 위어 마루 폭 L이 큰 경우.

위어 상류의 한 지점과, 위어에서 한계수심 나타나는 한 지점사이에 베르누이 정리 사용하여 유량 공식 유도.

$\begin{array}{cc}H=h+\frac{{V_a}^2}{2g}& =h_c+\frac{{V_c}^2}{2g}\\ & =\frac{2}{3}H+\frac{{V_c}^2}{2g}\\ \end{array}$

$V_c=\sqrt{\frac{2gH}{3}}$

$\begin{array}{cc}Q=b{h}_c{V}_c& =\frac{2bH}{3}\sqrt{\frac{2gH}{3}}\\ & =1.7b{H}^{\frac{3}{2}}\\ \end{array}$

사다리꼴 광정 위어

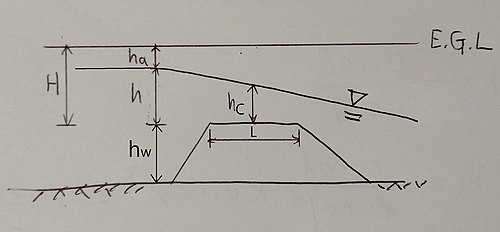
홈마 공식(실험에 의한 것)

$Q=Cb\sqrt{2g}{h}^{\frac{3}{2}}$

참고 문헌

• 틀:서적인용
• 틀:서적인용