압밀 예제

토질역학 목차 : 토질역학

e-log P 곡선 문제

예제 1

흙시료 건조 중량 120gf, 시료 초기높이 2.50cm, G_s=2.75, 시료 단면적 30cm²일 때 e-log p 곡선을 그리시오.

압력 p (kgf/cm²)	압밀 완료 시료 최종 높이 H(cm)
0	2.500
0.05	2.488
0.1	2.465
0.2	2.431
0.4	2.389
0.8	2.324
1.6	2.225
3.2	2.115

풀이

1. 공극 제외 흙시료 높이 H_s 계산

H_{s} = \frac{V_{s}}{A} = \frac{W_{s}}{A γ_{s}} = \frac{W_{s}}{A G_{s} γ_{w}} = \frac{120 g f}{30 c m^{2} \times 2.75 \times 1 g f / c m^{3}} = 1.4545 c m

2. 공극만의 초기높이 H_v 계산

H_{v} = H - H_{s}

계산해서 아래 표로 정리.

압력 p (kgf/cm²)	압밀 완료 시료 최종 높이 H(cm)	H_s	H_v
0	2.500	1.4545	1.04550
0.05	2.488	1.4545	1.03350
0.1	2.465	1.4545	1.01050
0.2	2.431	1.4545	0.97650
0.4	2.389	1.4545	0.93450
0.8	2.324	1.4545	0.86950
1.6	2.225	1.4545	0.77050
3.2	2.115	1.4545	0.66050

3. e 계산

압력 p (kgf/cm²)	압밀 완료 시료 최종 높이 H(cm)	H_s	H_v	$e = \frac{H_{v}}{H_{s}}$
0	2.500	1.4545	1.04550	0.71880
0.05	2.488	1.4545	1.03350	0.71055
0.1	2.465	1.4545	1.01050	0.69474
0.2	2.431	1.4545	0.97650	0.67136
0.4	2.389	1.4545	0.93450	0.64249
0.8	2.324	1.4545	0.86950	0.59780
1.6	2.225	1.4545	0.77050	0.52974
3.2	2.115	1.4545	0.66050	0.45411

가로축을 log 스케일로, 세로축을 e로 그래프를 그리면

파일:압력 공극비 그래프.PNG

Matlab 또는 GNU Octave로 계산하는 것은 Matlab/그래프#semilogx를 참조.

예제 2

G_s = 2.73, 초기 점토시료 두께 = 19.0mm, 최종순간 함수비 = 19.8%이고, 압밀시험결과가 다음과 같다고 하자.


압력(kPa)	0	54	107	214	429	858	1716	3432	0
24시간 후 다이얼게이지 읽음값(mm)	5.00	4.747	4.493	4.108	3.449	2.608	1.676	0.737	1.480

e - log σ' 그래프를 그리시오.

원래 $H_{s} = \frac{W_{s}}{A G_{s} γ_{w}}$ 를 이용해 먼저 H_s를 구하지만, 문제의 조건에서 알 수 있는 값은 G_s, γ_w(기지값)이므로 W_s, A를 몰라서 다른 방법으로 H_s를 구해야 한다.

흙의 삼상관계를 생각하여 H_s를 구해야 한다.

틀:-

포화된 점토시료(S = 1)에 대해 $e = w G_{s}$ 이므로 최종 상태의 값들을 대입하여 e_e를 알 수 있다.

e_{e} = w_{e} G_{s} = 0.198 \times 2.73 = 0.541

e_{e} = e_{0} - Δ e, e_{0} = e_{e} + Δ e = 0.541 + Δ e

\frac{Δ e}{1 + e_{0}} = \frac{Δ H_{e}}{19 m m} = \frac{5 - 1.48 m m}{19 m m}

\frac{Δ e}{1.541 + Δ e} = \frac{5 - 1.48}{19}

Δe = 0.35

e₀ = 0.541 + 0.35 = 0.891

e_{0} = \frac{H_{v}}{H_{s}} = \frac{H - H_{s}}{H_{s}} = \frac{19 - H_{s}}{H_{s}} = 0.891

∴ H_{s} = 10.048 m m

H_s를 구했다면 이제 각 단계별 e를 구해야 한다. e₁만 풀고 나머지는 반복 작업.

\begin{matrix} e_{1} & = e_{0} - Δ e_{1} \\ = e_{0} - \frac{5 - 4.747}{H_{s}} \\ = 0.891 - \frac{5 - 4.747}{10.048} \\ = 0.866 \end{matrix}

반복작업은 엑셀로 계산해서 그래프를 그린다.


압력(kPa)	24시간 이후 다이얼게이지 읽음(mm)	Δe	e
0	5		0.891
54	4.747	0.02517914013	0.8658208599
107	4.493	0.02527866242	0.8405421975
214	4.108	0.0383160828	0.8022261146
429	3.449	0.06558519108	0.7366409236
858	2.608	0.08369824841	0.6529426752
1716	1.676	0.09275477707	0.5601878981
3432	0.737	0.09345143312	0.466736465
0	1.48	-0.07394506369	0.5406815287

체적변형계수 계산 예제

완전 포화된 점토. 시료 초기 두께 20mm, 초기 함수비 24%, 비중 2.70, 시험결과 표는 다음과 같을 때, 체적변형계수 m_v 계산


재하하중(kPa)	시료 두께(mm)
0	20
25	19.806
50	19.733
100	19.600
200	19.357
400	18.835
800	18.167

$e_{0} = w_{0} G_{s} = 0.24 \times 2.7 = 0.648$


재하하중(kPa)	시료 두께(mm)	ΔH_f (mm)
0	20	0
25	19.806	0.194
50	19.733	0.267
100	19.600	0.400
200	19.357	0.643
400	18.835	1.165
800	18.167	1.833

$\frac{Δ e_{e}}{1 + e_{0}} = \frac{Δ H_{e}}{H_{0}}$

$\frac{Δ e_{e}}{1 + 0.648} = \frac{1.833}{20}$

$Δ e_{e} = 0.151 = \frac{Δ H_{e}}{H_{s}} = \frac{1.833}{H_{s}}$

$∴ H_{s} = 12.139 m m$

Δe_f값을 계산한다. $Δ e_{f} = \frac{Δ H_{f}}{H_{s}}$


재하하중(kPa)	시료 두께(mm)	ΔH_f (mm)	Δe_f
0	20	0	0
25	19.806	0.194	0.016
50	19.733	0.267	0.022
100	19.600	0.400	0.033
200	19.357	0.643	0.053
400	18.835	1.165	0.096
800	18.167	1.833	0.150

e 계산. $e = e_{0} - Δ e_{f} = 0.648 - Δ e_{f}$


재하하중(kPa)	시료 두께(mm)	ΔH_f (mm)	Δe_f	e
0	20	0	0	0.648
25	19.806	0.194	0.016	0.632
50	19.733	0.267	0.022	0.626
100	19.600	0.400	0.033	0.615
200	19.357	0.643	0.053	0.595
400	18.835	1.165	0.096	0.552
800	18.167	1.833	0.150	0.498

$m_{v} = \frac{\frac{Δ e}{Δ σ}}{1 + e}$


하중 증분(kPa)	Δe	Δσ	1+e	m_v (m²/kN)
0 ~ 25	0.016	25	1.648	0.000388
25 ~ 50	0.006	25	1.632	0.000147
50 ~ 100	0.011	50	1.626	0.000135
100 ~ 200	0.020	100	1.615	0.000124
200 ~ 400	0.043	200	1.595	0.000135
400 ~ 800	0.054	400	1.552	0.000087

어떤 책^[1]에서는 m_v 구할 때 분자의 1 + e에서 e를 쓰지 않고 하중 증분 단계의 평균 간극비 e_m을 쓰기도 함.

압밀침하량 예제

1차 압밀침하 예제 1

q=49kPa, e₀=1.1, γ_sat=1.84t/m³, H₀=10m인 포화점토층의 5m 깊이 1차압밀침하량 ΔH를 구하라. 단 P=9.2t/m²일 때 e=1.04이며, 지하수위는 지표면에 있고 점토층 하단은 암반으로 되어있다.

풀이

1차 압밀침하량은 $S_{c} = \frac{Δ e}{1 + e_{0}} H_{0} = \frac{e_{0} - e_{1}}{1 + e_{0}} H_{0}$

다른 값들은 주어져 있고, e₁만 구하면 된다.

P_{0} = (γ_{s a t} - γ_{w}) \frac{H_{0}}{2} = (1.84 - 1) \times 5 = 4.2 t / m^{2}

Δ P = q = 49 k P a = 5.0 t / m^{2}

P_{0} + Δ P = 9.2 t / m^{2}

압밀 이후 하중 $P_{0} + Δ P = 9.2 t / m^{2}$ 일 때 e=1.04라고 했으므로 e₁=1.04이다.

∴ S_{c} = \frac{e_{0} - e_{1}}{1 + e_{0}} H_{0} = \frac{1.1 - 1.04}{1 + 1.1} \times 10 m = 0.286 m

1차 압밀침하 예제 2

오른쪽 그림에서 가장 아래 점토층의 1차 압밀침하량을 구하시오. 토층 상단에 작용하는 하중은 8.0t/m²이다.

토층	종류	두께(m)	비고
1	순수 모래	1.5	$γ_{1} = 1.765 t / m^{3}$
2	포화 모래	3.0	G_s=2.65 e=0.7
3	정규압밀 포화 점토	5.0	$γ_{s a t 3} = 1.865 t / m^{3}$ e₀=0.9 w_L=60%

풀이

정규압밀 점토에 대한 1차 압밀침하량은 $S_{c} = \frac{C_{c}}{1 + e_{0}} H \log \frac{{\bar{p}}_{0} + Δ \bar{p}}{{\bar{p}}_{0}}$

액성한계 w_L이 주어져있으므로 경험식을 통해 압축지수 C_c를 구할 수 있다. 불교란 시료에 대해 $C_{c} = 0.009 (w_{L} - 10) = 0.009 (60 - 10) = 0.45$

H=z₃=5.0m

$Δ \bar{p} = 8.0 t / m^{2}$

점토층 중간 지점( $\frac{z_{3}}{2}$ )의 ${\bar{p}}_{0}$ 만 구하면 된다. 단위중량을 이용하면 되는데 주의할 점은 물이 받는 응력을 제외한 흙만이 받는 응력만을 계산에 포함시켜야 한다. 즉

{\bar{p}}_{0} = γ_{1} z_{1} + γ_{s u b 2} z_{2} + γ_{s u b 3} \frac{z_{3}}{2}

$γ_{s u b 2} = γ_{s a t 2} - γ_{w} = \frac{G_{s} + e}{1 + e} γ_{w} - γ_{w} = \frac{G_{s} - 1}{1 + e} γ_{w} = \frac{2.65 - 1}{1 + 0.7} \times 1 = 0.971 t / m^{3}$

$γ_{s u b 3} = γ_{s a t 3} - γ_{w} = 1.865 - 1 = 0.865 t / m^{3}$

$∴ {\bar{p}}_{0} = 7.723 t / m^{2}$

최종적으로 침하량을 구하면 $S_{c} = 0.3656 m$

1차 압밀침하 예제 3

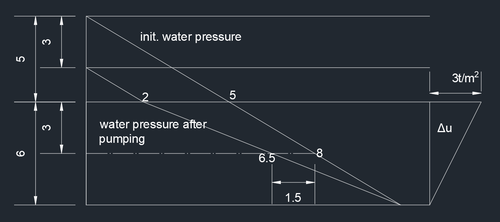
양수작업으로 인해 국부적으로 지하수위 하강 시

양수작업 때문에 지하수위가 지표면에 위치하다가 3m 하강했을 때 압밀침하량 계산하기.

틀:-

침하량 식 $S_{c} = \frac{C_{c}}{1 + e_{0}} H \log \frac{{σ_{0}}^{'} + Δ σ}{{σ_{0}}^{'}}$ 에서 Δσ가 변한다. 과잉간극수압이 소산되면서 σ'은 증가하게 된다.

넓은 범위에 걸쳐 지하수위가 하락했을 때의 수압분포. 지하수위 하강으로 인한 단위중량 변화를 무시했을 경우
양수 이후 수압분포

이때 점토층 중앙에서 과잉간극수압 Δu = 1.5t/m²이고,

σ_{0}' = (1.9 - 1) \times 5 + (1.85 - 1) \times 3 = 7.05 t / m^{2}

이므로

S_{c} = \frac{0.43}{1 + 0.9} \times 6 m \times \log \frac{7.05 + 1.5}{7.05} = 0.114 m

단위중량 차로 인한 유효응력 감소분까지 고려한다면 점토층 중앙에서 지하수위 하강 후 전응력

σ_{1} = 1.8 \times 3 + 1.9 \times 2 + 1.85 \times 3 = 14.75 t / m^{2}

같은 지점에서 지하수위 하강 후 압밀완료 시 수압

u₁ = 6.5t/m²

같은 지점에서 지하수위 하강 후 유효응력

σ_{1}' = σ_{1} - u_{1} = 8.25 t / m^{2}

∴ S_{c} = \frac{0.43 \times 6 m}{1 + 0.9} \log \frac{8.25}{7.05} = 0.0927 m

역시 로그 뒷부분만 변한다.

광범위한 지하수위 하강 시

σ₀'은 동일. Δσ를 다르게 계산해야 함.

이땐 $Δ σ = γ_{w} \cdot 3 m = 3 t / m^{2}$

또는 이렇게 볼 수도 있다.

\begin{matrix} {σ_{1}}^{'} & = {σ_{0}}^{'} + Δ σ \\ = γ_{s a t - s} \times 3 m + γ_{s u b - s} \times 2 m + γ_{s u b - c} \times 3 m \\ = 1.9 \times 3 + 0.9 \times 2 + 0.85 \times 3 \\ = 10.05 t / m^{2} \end{matrix}

이는 $σ_{0}' + Δ σ = 7.05 + 3 = 10.05 t / m^{2}$ 과 동일함을 확인 가능하다.^[2]

근데 이거 다른 책^[3]에서도 이런가? 지하수위는 하강했어도 지하수위 위의 흙은 포화상태라는 조건이 붙어있어야 이렇게 하는 거 아닌가? 단위중량차 고려 안해서 그런 것 같네

예제 4

정규압밀점토 침하량이 S_c라 할 때, 문제에서 60% 압밀 침하량이 얼마냐고 물어본다면 반드시 마지막에 0.6S_c라고 답해야 한다.

예제 5

무한등분포하중이 작용하는 점토층에 압밀이 진행중일 때의 연직유효응력을 묻는 경우. 전응력 = 유효응력 + 공극수압으로 푸는 게 아님. 압밀도와 과잉간극수압, 유효응력 사이의 관계를 이용해야 한다.

Δ σ^{'} = Δ σ \cdot U_{z} = Δ u_{0} \cdot U_{z}

σ^{'} = {σ_{0}}^{'} + Δ σ^{'}

그리고 깊이에 따라 연직유효응력 구해서 그래프 그리라는 문제에서 σ' 서로 다른 값 써야된다! z가 달라지면 σ'도 달라져!

2차 압밀침하 예제 1

1차 압밀침하 예제 2의 그림에 대해, 4년 후에 1차 압밀이 완료되며, 4년부터 10년까지 2차 압밀이 일어난다고 하자. 10년 후 전체 압밀침하량은? 단, 2차 압축지수 C_a=0.020이라고 한다.

풀이

정규압밀점토에 대해 2차 압밀량을 구한다. $S_{s} = \frac{C_{a}}{1 + e_{p}} H \log \frac{t_{2}}{t_{1}}$ 에서 e_p를 구한다. (얕보지 마라 이거 적어놓고 또 틀렸다)

e_{0} - e_{p} = Δ e = C_{c} [\log ({\bar{p}}_{0} + Δ \bar{p}) - \log \bar{p}]

∴ e_{p} = e_{0} - C_{c} [\log ({\bar{p}}_{0} + Δ \bar{p}) - \log \bar{p}] = 0.9 - 0.45 [\log (7.723 + 8.0) - \log 7.723] = 0.761

S_{s} = \frac{0.020}{1 + 0.761} 5.0 \log \frac{10}{4} = 0.022597 m

전체 압밀침하량은 1, 2차 압밀침하량을 더해서 구한다. 0.3656 + 0.022597 = 0.38820 m

압밀 시간에 대한 예제

log t법, $\sqrt{t}$ 법을 쓸 때는 시료의 평균 높이를 쓴다. $\sqrt{t}$ 법할 때 t = 0에서 초기압축이 있었다면 그걸 반영해서 시료 평균 높이를 구해야 함. 배수거리 구하는 거.

공사 시간 계산

또 틀림

하부가 투수층인 8m 두께 점토층 원지반 위에 5m 높이로 성토하였다. 원지반 m_v = 0.5 m²/MN, c_v = 10m²/yr이다. 성토 완료 후 성토층 상부면 허용 침하량이 50mm이다. 그렇다면 성토 공사는 얼마나 빨리 완료할 수 있을까? 성토층 전체 단위중량은 2200kg/m³이다. 성토하중은 모든 영역에서 즉시 작용한다고 가정한다.^[4]

성토층 단위중량

γ = 2200 k g / m^{3} \times 9.8 m / s^{2} = 21.56 k N / m^{3}

성토로 인한 응력 증가량

Δ σ = 21.56 k N / m^{3} \times 5 m = 107.8 k N / m^{2}

침하량

\begin{matrix} S_{c} & = Δ σ \cdot m_{v} \cdot H \\ = 107.8 k N / m^{2} \times 0.5 m^{2} / M N \times 8 m \\ = 0.4312 m \end{matrix}

이대로 압밀이 진행되면 성토층 상부 높이는 원지반에서 5 - 0.4312 = 4.5688m가 되어버린다. 이를 해결하기 위해 이렇게 생각해본다. z만큼 추가로 더 성토하고, z만큼이 침하된다면 결국 원지반으로부터 성토층 상부 높이가 5m가 될 것이다. 이 z를 구한다.

z를 더 성토하면 응력 증가량도 증가한다.

Δ σ = (5 + z) \times 21.56 k N / m^{2}

침하량

\begin{matrix} z & = Δ σ \cdot m_{v} \cdot H \\ = (5 + z) \times 21.56 k N / m^{2} \times 0.5 m^{2} / M N \times 8 m \end{matrix}

$∴ z = 0.472 m$

이제 성토공사 완료까지의 시간을 구할 것이다. 0.472m만큼이 다 침하되면 원하는 목표인 5m 성토가 완료된 것이다.(압밀도 = 100%) 그러나 허용침하량이 0이 아니라 0.050m이기 때문에 5 + 0.050 = 5.050m 높이까지만 압밀이 진행되었더라도 공사가 완료된 것으로 간주할 수 있다. 따라서 이때의 압밀도를 먼저 구한다.

U_{a v g} = \frac{0.472 - 0.050}{0.472} = 0.894

즉 89.4% 압밀이 완료되었을 때 성토공사가 완료되었다고 볼 수 있다. 이제 89.4% 압밀에 걸리는 시간을 구한다.

\begin{matrix} T_{v} & = 1.781 - 0.933 \log (100 - U_{a v g} (%)) \\ = 0.824 \end{matrix}

$\begin{matrix} t & = \frac{T_{v} \cdot {H_{d r}}^{2}}{c_{v}} \\ = \frac{0.824 \times 4^{2} m^{2}}{10 m^{2} / y r} \\ = 1.32 y e a r s \end{matrix}$

sand seam이 있는 예제

C_c = 0.323, e₀ = 0.855일 때

전체 침하량은 sand seam이 있을 때나 없을 때나 같다.^[5]

그 과정은 아마 이럴 듯.

$\begin{matrix} σ_{{0_{1}}^{'}} & = 17 \times 2 + (19 - 9.8) \times 6 + (20 - 9.8) \times \frac{4.5}{2} \\ = 112.15 \end{matrix}$

$S_{c_{1}} = \frac{0.323}{1 + 0.855} \times 4.5 \log \frac{112.5 + 60}{112.5} = 0.146 m$

$\begin{matrix} σ_{{0_{2}}^{'}} & = 17 \times 2 + (19 - 9.8) \times 6 + (20 - 9.8) (4.5 + \frac{1.5}{2}) \\ = 142.75 \end{matrix}$

$S_{c_{2}} = \frac{0.323}{1 + 0.855} \times 1.5 \log \frac{142.5 + 60}{142.5} = 0.0398 m$

$S_{c_{1}} + S_{c_{2}} = 0.186 m$ (sand seam 없을 때와 동일)

그러나 3년 후 침하량은 달라진다.

풀이 과정은 각 구간의 T_v₁, T_v₂를 구하고, (조건으로 C_v = 1.26m²/yr)

$T_{v} = 1.781 - 0.933 \log (100 - U_{a v g})$ 식으로 U_avg₁, U_avg₂를 구한 뒤,

$U_{a v g} = \frac{4.5 m \times U_{a v g_{1}} + 1.5 m \times U_{a v g_{2}}}{6 m}$ 를 해서 U_avg를 구한 뒤에 총침하량에 곱해서 3년 후 침하량을 구한다.

각주

↑ 서상열, 김학삼 <<토질역학>> 272쪽
↑ 장연수, <<토질역학>>, 234쪽
↑ 이인모 <<토질역학의 원리>>
↑ Graham Barnes, <<Eurocode에 근거한 토질역학 이론과 실습>>, 185쪽
↑ 이인모, <<토질역학의 원리>>, 343쪽

참고 문헌

장병욱; 전우정; 송창섭; 유찬; 임성훈; 김용성 (2010). 《토질역학》. 구미서관. 틀:ISBN.
이인모 (2013). 《토질역학의 원리》 2판. 씨아이알. 311-312, 317쪽. 틀:ISBN.

[1] 서상열, 김학삼 <<토질역학>> 272쪽

[2] 장연수, <<토질역학>>, 234쪽

[3] 이인모 <<토질역학의 원리>>

[4] Graham Barnes, <<Eurocode에 근거한 토질역학 이론과 실습>>, 185쪽

[5] 이인모, <<토질역학의 원리>>, 343쪽

[1]

[2]

[3]

[4]

[5]