토목기사 요약/응용역학/힘과 모멘트

• 자유물체도: 분리된 한 물체와 타물체가 그 물체에 작용하는 힘을 나타낸 그림(90)

힘의 평형

♣♣♣

90 산업기사 기출문제지만 기사에도 이런 유형 나옴

네 힘의 합력이 왼쪽 끝에서 400만큼 떨어진 곳에 위로 300만큼이라면 그림에서 F, P를 구하시오.

풀이

합력이 위로 300이니까 평형이려면 아래로 300을 작용시켜서 계산해야함. F에서 모멘트 합력이 0임을 이용.

$-100\times 200+200\times 300+300P-500\times 200=0$

$P=200$

다음으로 F만이 미지수이기 때문에 세로 방향 힘의 평형을 이용한다.

$-100+F-200+200=300$

$F=400$

모멘트

♣♣♣

92 기출

한 점에 작용하지 않는 힘을 원점으로 이동해 합성하면 그림과 같다. 원점에 대한 편심거리 e는?

---

풀이

R e = M. e = 10 / 10 = 1m

---

94, 97 기출, 14-2 유사

R, θ, M 구하기.

---

풀이

수평력 $R\cos \theta +25-80=0$

$R\cos \theta =-25+80=55$

수직력 $R\sin \theta =10$

$\therefore R=\sqrt{55^2+10^2}=55.9kgf$

또한 $\tan \theta =\frac{10}{55},\theta =10.3^{\circ }$

$\mathrm{\Sigma }{M}_R=0$임을 이용하여 M을 구한다.

$-10\times 20+80\times 40+M=0$

$\therefore M=-3000kgf\cdot m$

---

79, 80

P의 힘으로 열차를 끌기 시작했다. A점의 연직반력 R_a?

---

풀이

ΣM_B = 0임을 이용하면 $R_a=\frac{W}{2}-\frac{P\cdot b}{2a}$

---

92, 13-2, 17-4

그림에서 R_A 크기를 W로 나타내시오.

---

풀이

아래쪽 반력의 작용점에서 모멘트의 합이 0임을 이용한다.

$R_A\times r\sin 60^{\circ }-W\cdot r\cos 60^{\circ }=0$

$R_A=\frac{Wr\cos 60^{\circ }}{r\sin 60^{\circ }}=\frac{W}{\sqrt{3}}=0.577W$

힘의 합성

♣♣

한 점에 작용하는 두 힘의 합성 : 힘의 사변형 법칙, 삼각형 법칙 사용.

$P=\sqrt{{P_1}^2+{P_2}^2+2P_1{P}_2\cos \alpha }$

• α : 사잇각

힘의 분해

♣♣♣

95, 00, 20-1+2 기출

1600과 600 힘의 합력은 R과 같다. R의 크기는?

풀이

1600, 600을 R의 좌표계(?)에 맞게 분해해준 뒤, 구하려고 하는 방향의 힘만 더해서 구해주면 됨.

$R=1600\cos 30^{\circ }+600\cos 60^{\circ }=1686$

트러스 문제

84, 87, 96 기출, 14-2 유사

두 부재가 받는 힘은? 오른쪽 끝에서 당기는 힘은 1000이다.

풀이

위의 부재는 인장되고 아래 부재는 압축될 것이다. 여기에 따라 가상의 힘 P_A, P_B를 도입한다. P_A는 횡방향 힘만 있으므로 그냥 두고, P_B는 대각선으로 작용하니까 수직, 수평방향으로 분할한다. 그림으로 나타내면 다음과 같다.

이제 가로, 세로 방향 힘의 평형을 이용해서 P_A, P_B를 계산. P_A = 1732(인장), P_B = 2000(압축)

91, 95, 18-1 기출

A 부재 축방향력은?

풀이

트러스 단면법이라고 생각하면 된다.

A에 작용하는 축력을 P라고 하고 P를 가로, 세로로 분해한다. O점에서 모멘트 합을 취해보면

$P\sin 60^{\circ }1000\tan 30^{\circ }-500\cdot 1200=0$

$\therefore P=1200$

90

D가 받는 힘은?

풀이

ΣV = 0이므로 D = 0

케이블 문제

92, 93, 99, 01, 16-2, 19-3, 20-1+2

P를 a와 W로 나타내시오.

풀이

$P\cos \frac{a}{2}=\frac{W}{2}$

$\therefore P=\frac{W}{2\cos \frac{a}{2}}$

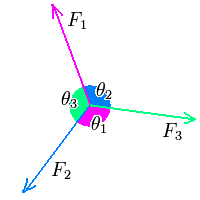
라미의 정리

19-2

Lami's theorem.

$\frac{F_1}{\sin {\theta }_1}=\frac{F_2}{\sin {\theta }_2}=\frac{F_3}{\sin {\theta }_3}$

마찰력

97

경사각 30도, W = 4tf인 물체를 P의 힘으로 밀어올렸다. 마찰계수는 0.3일 때 P는 최소 얼마여야 하는가?

풀이

W를 경사면에 따라 분리한 힘은 W sin θ = 2tf, 경사면에 수직인 수직항력은 W cos θ이다.

마찰력은 마찰계수에 수직항력을 곱한 값이므로 0.3 × W cos θ = 1.04tf이다.

따라서 P는 최소 2 + 1.04 = 3.04tf이어야 물체가 움직인다.